1.5 Il quarto problema di Roberto:
e se il moto non è rettilineo?
Roberto ormai sa che basta guardarsi intorno con attenzione per individuare nella realtà quotidiana gli esempi desiderati. Questa volta l’ispirazione gli viene guardando l’orologio appeso in cucina.
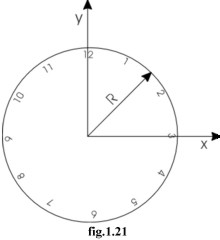Se osserviamo la lancetta dei secondi si nota che la punta descrive una traiettoria circolare, ma nessuno può contestare che il suo moto sia uniforme (Δs/Δt=cost)!
Abbiamo così individuato un moto uniforme non rettilineo.
Roberto si accinge a studiarne le caratteristiche.
Assume come sistema di riferimento il sistema cartesiano ortogonale con origine nel centro (vedi fig.1.21). Indica con R la lunghezza della lancetta dei secondi, che equivale al raggio della circonferenza descritta dalla punta (*).
Essendo il moto uniforme l’equazione oraria s(t) è data da
Nel caso considerato T=60s, la misura della lunghezza della lancetta R=25cm.
La legge oraria è espressa da s=2,62t, con t in secondi e s in centimetri. La velocità della punta in ogni punto della circonferenza è v=2,62cm/s.
Anche la lancetta ruota descrivendo angoli uguali in tempi uguali. Se 2π è l’angolo giro espresso in radianti e T il periodo (tempo impiegato a compiere un giro) otteniamo la velocità angolare (angolo descritto nell’unità di tempo)
Anche la velocità angolare è una grandezza vettoriale: ω è l’intensità, la direzione coincide con l’asse di rotazione, il verso indica il senso di rotazione (orario o antiorario).
La velocità della punta, che è indicata anche come velocità periferica, si può anche esprimere come
Ma la velocità è una grandezza vettoriale e quindi occorre anche indicare la direzione e il verso.
La direzione della velocità è data dalla tangente alla traiettoria nel punto considerato, quindi perpendicolare al raggio, e il verso è quello dello spostamento.
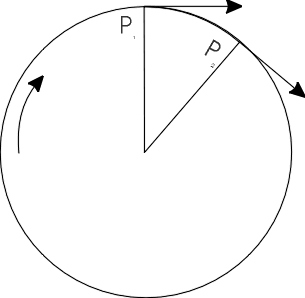Roberto disegna i vettori velocità in P1 e P2.
Riflettendo gli sorge un dubbio: è vero che la velocità in ogni punto ha lo stesso valore e il moto lungo la circonferenza è uniforme, ma in P2 la direzione è diversa che in P1.
Se c’è una variazione di velocità, allora ci deve essere una accelerazione!
Roberto si trova in difficoltà e allora ricorre al fratello Andrea, che non solo è quasi un genietto nelle materie scientifiche, ma ha anche una qualità rara: è molto paziente e disponibile.
Andrea gli conferma che se c’è variazione di velocità, anche se è solo la direzione a cambiare, c’è una accelerazione e gli spiega come fare per calcolarla.
Traccia i vettori velocità che corrispondono a degli intervalli di tempo uguali, facendo partire la loro origine dallo stesso punto. Se il vettore ruota di un piccolo angolo, la variazione di velocità è rappresentata dalla base di un triangolo isoscele.
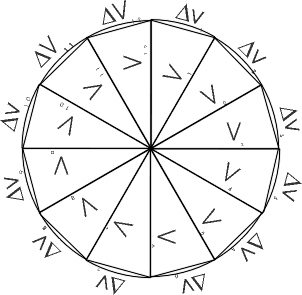Traccia poi le variazioni di velocità corrispondenti a una rivoluzione completa. La somma dei loro valori è uguale alla somma dei lati del poligono rappresentato. In realtà la direzione cambia costantemente e l’approssimazione sarà tanto maggiore quanto più piccolo è l’angolo del triangolo che noi scegliamo. Più i lati del poligono sono corti, più quest’ultimo si confonde con una circonferenza di raggio v.
Per questo motivo la somma dei valori assoluti delle variazioni di velocità durante una rivoluzione è data dalla lunghezza della circonferenza 2πv. L’accelerazione quindi si ottiene dividendo per T:
Inoltre si osserva che più l’angolo al vertice dei triangoli isosceli è piccolo, più l’angolo formato fra la variazione di velocità e la velocità si avvicina a 90°. L’accelerazione del moto circolare uniforme è dunque diretta perpendicolarmente alla velocità e poichè la velocità è diretta secondo la tangente alla traiettoria, l’accelerazione non può che essere diretta lungo il raggio e verso il centro. Per questo motivo l’accelerazione prende il nome di accelerazione centripeta.
* Se hai studiato la geometria analitica puoi osservare che l’equazione della circonferenza rappresenta anche l’equazione della traiettoria: x2+y2=R2
Torna al testo.