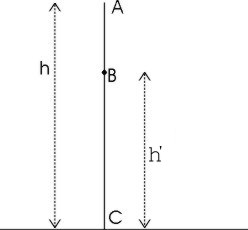
3.2 Conservazione dell’energia meccanica

Supponiamo ora di avere un corpo ad una altezza h dal suolo e di lasciarlo cadere a terra nel punto C (fig.3.14). Come varia la sua energia meccanica durante la caduta?
Trascuriamo la resistenza dell’aria.

fig.3.14

Se assumiamo che la sua energia potenziale in C sia nulla, nel punto A abbiamo E_{A p}=mgh.
Nel punto C si ha solo energia cinetica E_Cc=mv_C ²/2. Poiché la velocità acquistata nella caduta è v=√2gh si ottiene mv_C²/2=mgh, quindi l’energia cinetica in C equivale all’energia potenziale iniziale.
Consideriamo il punto intermedio B. Nel punto B l’oggetto possiede sia energia potenziale E_{B p}=mgh’ sia energia cinetica. Infatti cadendo dalla altezza h ha acquistato una velocità v_B=√2g(h-h’): E_Bc=mv_B²/2=2mg(h-h’)/2=mg(h-h’).
L’energia meccanica totale è E_B=E_c+E_p=mgh.
Poiché B è un punto qualsiasi della traiettoria possiamo affermare che:

Se non ci sono forze dissipative l’energia meccanica totale si conserva.

Questo risultato, ricavato in questo caso particolare di una caduta nel vuoto si estende in generale come Principio di conservazione dell’energia meccanica. Esso è valido solo quando non sono presenti forze dissipative (come gli attriti).