
|
3.3 Calcolo di alcuni momenti di inerzia Ecco alcuni esempi di momenti di inerzia:
|

|
I=2mR2/5 |

|
I=2mR2/3
|
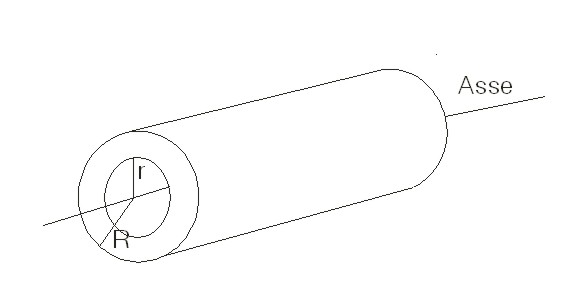
|
I=m(r2+R2)/2
|
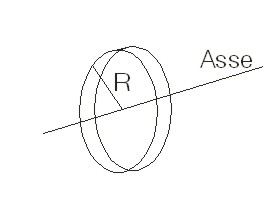
|
I=mR2 rispetto ad un asse passante per il baricentro, lungo un suo diametro (fig.3.27): |

|
I=mR2/2
|
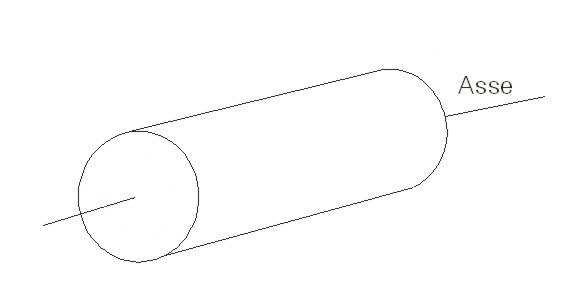
|
I=mR2/2 rispetto ad un asse passante per il baricentro e perpendicolare all’asse del cilindro (fig.3.29): |

|
I=mR2/4+ml2/12
|

|
I=ml2/12
|

|
Per trovare il momento d’inerzia I di un corpo rispetto ad un asse qualunque si applica il teorema di Huygens-Steiner: |
