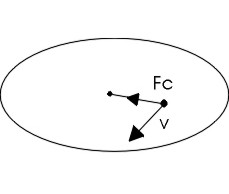
3.1 Problema di Vladimir
(e il giradischi)
Se noi poniamo un piccolo cubo di legno sulla piattaforma di un giradischi vicino all’asse di rotazione, il cubo ruoterà con il piatto. Se poniamo il cubo a distanza sempre maggiore dall’asse, arrivato a un certo punto non rimane più sul piatto, ma ne viene gettato fuori. Questa esperienza ci permette di misurare il coefficiente di attrito fra legno e superficie del piatto, usando solo un riga graduata?